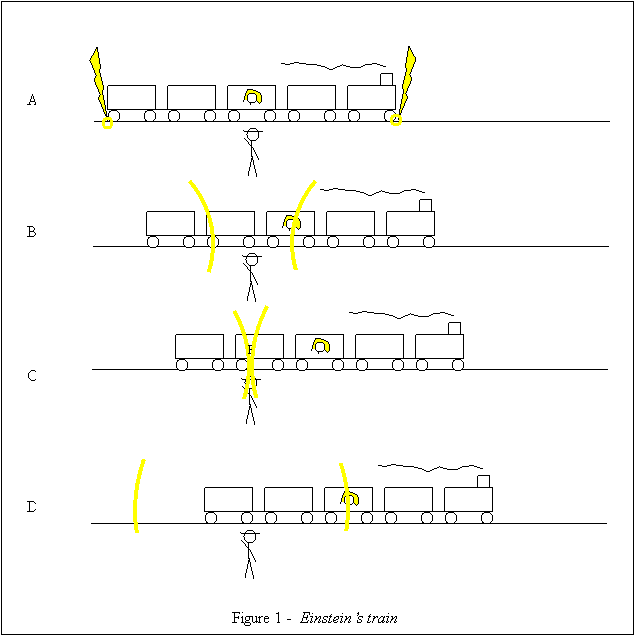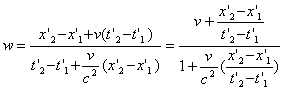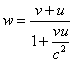| Home | English | Hebrew |
|
Understanding Special Relativity Table of Content
Understanding Special Relativity
By Rafi Moor 2004
The purpose of this article is to introduce the theory of special relativity in an easily understandable way. It reviews the basic issues in special relativity in a somewhat informal way, without the use of higher mathematics, so that anyone with a basic knowledge of physics can easily understand it.
When the wavelike nature of light (and other electromagnetic radiation) was discovered at the 18th, century scientists assumed that there must be some kind of substance in which the waves move. They believed that space was filled with such a substance, and called it ether. In 1887 Albert Michelson and Edward Morley carried out an experiment in which they tried to show the motion of Earth relative to the ether by measuring changes in light speed in different directions. To their astonishment they found no change in the light speed regardless of the relative motion between Earth and the source of light or the ether. As a result of this experiment known as the Michelson Morley experiment, the theory of ether was abandoned by most physicists. In the absence of ether there was also no absolute reference to determine what is at rest and what is moving in space. This was where Einstein started his work on relativity.
Einstein based his theory on 2 simple postulates:
The laws of physics are the same in all inertial frames of reference.
The speed of light in vacuum has the same value c in all inertial frames of reference.
The first postulate claims a symmetry or equivalence between all inertial (not accelerating) frames. Any inertial frame can be assumed at rest and look at other inertial frames as moving in constant speed along straight lines. Another important point is that without an absolute reference there is also no absolute definition for a point or a place in space. What is a fixed point in space for one frame is a moving point for another frame. People on two frames that are moving relative to each other will not agree about the place where an event has happened in the past. The second postulate is the one that forces us to change the laws of physics as they were known before relativity. Imagine two spaceships pass near each other. One is headed to the sun and the other away from the sun. They both watch a single photon coming from the sun. Without relativity, after one second they both see the photon one light second away from the ship. Since the ships have moved away from each other by this second, they would see the photon in two different places at the same time. To see how we can settle this, let us look at an example presented by Einstein himself.
The Relativity of Simultaneity
Suppose there is a train moving in a constant speed along a straight track. A woman is standing exactly in the middle of the train. A man is standing on the ground outside the train. Now, the following scenario is described as seen or measured, or actually happening from the man’s point of view: Just when the woman is in front of him two lightning bolts strike both ends of the train. They leave marks on the train as well as on the track. The light from the lighting bolts starts to spread in a constant speed in all directions as shown in figure 1A. A fraction of a second later the light coming from the front of the train reaches the woman as shown in 1B. A little later the light coming from both lightning bolts reach the man simultaneously as shown in 1C. A little later yet the light from the rear reaches the woman.
The following phrases are true in the man’s frame:
Now, let’s try to figure out how things happen in the woman’s frame. There is one difference we already know: In the man’s frame the place where the events of the lightning bolts occur are the points on the track where they left their marks. In the woman’s frame the points are at the edges of the train. Thus, in her own frame, the woman is at all times in the same distance from the points where the lightning bolts hit. If we assume that all the phrases above are also true in the woman’s frames, there will be a logical contradiction: Light cannot go through equal distances in the same speed and yet not in the same period of time. So, at least one of the four phrases (any of them) must be wrong in the woman’s frame. If we were talking not about light but about two pieces of metal that are sprayed by the lightning bolts, then phrase c. would not be true in the woman’s frame. If the speed of the two pieces is the same and equals to v in the man’s frame, in the woman’s frame the speed of the piece coming from the front will be v + V and the speed of piece from the back will be v – V, where V is the speed of the train. But from postulate 2 we know that this is not the case when we talk about light. The speed of light remains constant regardless of the reference frame. So, one of the other three phrases must be wrong in the woman’s frame. Suppose it is d. That is, while the man measures the light from the front getting to the woman before the light from the back, the woman sees the light from both sides simultaneously. This could lead to very strange consequences: Suppose we put two photoelectric cells at point P on the train where the two flashes of light meet in the man’s frame. One of the cells is directed to the front of the train and the other to the back. Now we connect the cells to a bomb in a way that if the two cells are illuminated simultaneously the bomb explodes. In the man’s frame the bomb will explode. In the woman’s it will not since in her frame the flashes meet by her and not at point P. This will be very hard to settle. Remember that it is very easy to move from one inertial frame to another. All you need is some acceleration. Imagine the man sitting in a bar the next day when the woman enters. “How come you are here alive?” asks the man surprisingly, "I saw your train exploding to pieces yesterday. There were no survivors." “What are you talking about?” says the woman. “The train got safely to its final station where I got off." We can see that a solution that results in different material state in two inertial frames is not a good one. We can show similar problem if we try the solve the contradiction by claming that a. is not true in the woman’s frame and while the man measures equal distances between her and the edges of the train, in her own frame she is closer to the front of the train. Suppose there is a long stick lying on the train’s floor from the woman’s feet up to the front of the train. The woman takes the stick and tries to use it to push the emergency stop button on the rear end of the train. In her frame it is too short and the train goes on. But in the men’s frame the stick is long enough and the train stops. So, we are left with phrase b. We must assume that in the woman’s frame the lightning in the front happens before the one in the back. The only problem with this solution is that it sounds very weird. We use to think about time as absolute and independent of a reference frame. What happens now happens now, no matter from where you are looking. But let’s not forget how weird it sounds when we are first told that Earth is round, and far below us people stand with their feet towards us and call the direction pointing to us "down". In the small part of Earth surface that we cover in everyday life the curvature of it is so small that it can be considered flat. In the same way, for the low speeds we experience in everyday life, time can be considered absolute. But when we talk about higher speeds we see that this is not. We got now to one of the laws of relativity - the relativity of simultaneity. Two events that are simultaneous in one frame have time difference in another frame. Two clocks that are synchronized in one frame show different time in another frame. We can show from the above example that this difference grows with the relative speed between the tow frames and also with the distance between the two events in the direction of the relative motion. Now we have to see what else is relative to the reference frame.
Imagine two people on a dock trying to measure the length of a ship that is sailing along the dock. One is walking near the bow and the other by the stern. When the one in the front whistles, they mark both ends of the ship on the dock with a piece of chalk and then they measure the distance between the two marks. This works fine. But what if a single person tries to do the same? He marks one end of the ship, runs to the other end and marks it too. Since the ship moves while he runs, his measure will be either more or less than the ship’s length, depending on where started. In order to get the length of something we need to know where it’s two ends are simultaneously. But what if simultaneity is relative? Apparently we will measure a different length from different frames. Let’s go back to the train case. The man sees two lightning bolts happen simultaneously at both ends of the train. They leave marks on the track. For him the distance between the marks equals to the length of the train. The woman, in her frame, sees the track moving to the left of the drawing. The lightning in the right happen in her frame first and marks the position of the front end of the train on the track. The lightning at the left marks the rear end of the train a little later. During this time the track with the first mark on it has moved a little to the left. So in the woman’s frame the distance between the marks is less than the train length. What will we measure if we put the train and the track in the same inertial frame, like when the train stops? The length of an object in its own frame is called the proper length. Suppose the proper length of the train is equal to the proper distance between the marks on the track. This breaks the symmetry required by postulate 1: In the man’s frame the length of the train is its proper length. But in the woman’s frame the distance between the marks is shorter than its proper length. What if the proper length of the train is less than the proper distance between the marks? The man sees the train longer than its proper length and the woman sees the distance on the track shorter than the proper distance. Again, no symmetry. The only possibility that preserves symmetry is that the train’s proper length is longer than the proper distance between the marks. Both the man and the woman see the length on the other frame shorter than its proper length. This is another law of relativity – length contraction. When we measure distance on an inertial frame that is moving relative to us, the distance in the direction of the relative motion will be less than its proper distance.
Let’s build a light clock. We place two perfect reflecting mirrors face to face in a distance of exactly one light microsecond. We send a light pulse so that it goes back and forth between the two mirrors. Every tick of the clock is exactly one microsecond. Now, what we see if we look at our light clock from a frame that is moving relative to the clock’s frame in a direction perpendicular to the motion of the light as shown in figure 2. Relative to the second frame the distance that light passes while moving from one mirror to the other, is more than one light microsecond. Since light speed is constant, it would take the light more than one microsecond to go from mirror to mirror. So, while for a man on the clocks frame one microsecond passes every tick of the clock, for the man on the other frame it is a longer time. Or, the man in the other frame sees time pass “slower” for the man in the clock’s frame.
Symmetry requires also that the man on the clock’s frame sees time pass slower for the man on the other frame. This is a little hard to perceive. Because we are so used to think of time as absolute, it is much easier for us to accept that for two frames a length measured in each frame looks shorter to the other frame, than accepting that time measured in each frame looks longer in the other frame. We must understand that time is a different thing for every frame. It is not the same thing that looks different from every frame. We can make the following analogy: Two people start walking from the same point facing two different directions with an angle α between them as shown in figure 3. They both are walking forward at the same speed. After a while they look aside to see where the other person is. They both see that relative to the direction they walk the other is aligned with a point on their path they have already passed, so they both decide that the other is behind them. This is because forward and backward is a different thing for each one. In just the same way earlier and later are different things for two people that are in motion relative to each other. When they look at time on the other frame, they compare it to their own time. Like the two people that each sees the other behind him, the people on the moving frames both sees the other’s time pass slower.
We have seen now the three basic principles of Special Relativity: Length contraction, time dilation and simultaneity relativity. Now we need the mathematics of all this. For this purpose we will introduce the concept of time-space.
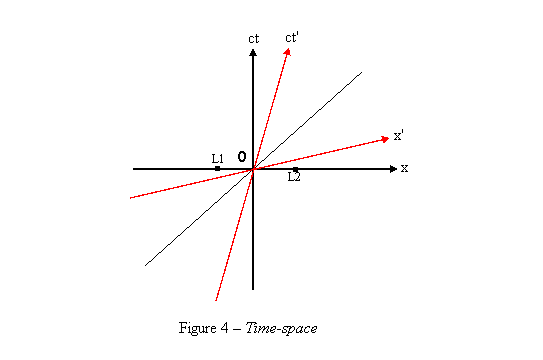
For anything happening in the world we can ask where it happened and when it happened. The answer to the first question positions the event in space and the answer to the second positions it in time. To position something in space we usually use an orthogonal coordinate system with three perpendicular axes and a common origin. To position something in time we need a reference point in time and a number that represent the time difference between the reference point and the event in question. The idea of time-pace is to combine these two things into one. We use a four dimensional coordinate system with three space axis and one time axis. The position of an events in it gives the answer to the where and when questions. Many times, when dealing with time-space, the units of length and time are chosen so that light speed c is 1, as with light-years and years. This gives a comfortable symmetry in the geometry of time-space. The problem with doing so is that it makes the equations we use unit dependent. We will use here a different trick. Instead of showing the time t on the fourth axis we will show the value of ct (time multiplied by light speed). This will represent time well because technically we just multiply the time t by a constant, which is just like choosing a different unit for time. By doing so, we get the wanted symmetry without making the equations unit dependent. And there is more to it: The units of ct are actually length units, so that we can use the same units for all our four time-space dimensions. Four dimensional time-pace is very hard to visualize. To make things more visual we will use only two or even one space dimensions to form a three or two dimensional time-space. Two dimensional time-space is enough for things that happen along a line as with the train example. The whole thing about relativity is how things look (or are) from different reference frames. The meaning of it is a transformation of events from one space-time coordinate system to another. We know how to transform points from one space coordinate system to another, but the mathematics or geometry of time-space is different from the Euclid geometry we use for space. Let’s draw two dimensional time-space coordinates axes x and ct as shown in figure 4. Suppose these are the time-space coordinates of the ground in the train example where the origin O is the point where the man stands at the moment the woman is in front of him.
The red line marked as ct’ shows the position of the woman as seen from the ground. This line can be described by the equation:
We define β as the ratio between the relative speed of the two frames and light speed:
β = v/c (1)
In the train’s coordinate system the woman is always at point x' = 0, so this line is actually the ct' axis of the train’s coordinates system. We know that for space, if one of the axes of a coordinate system is rotated by an angle α relative to another coordinates system, the other axis will be rotated at the same angle in the same direction. Is this also true in time-space? We know that on earth’s frame the two lightning bolts occurred at t = 0. We’ll mark them as points L1 and L2 on the coordinate system. On the train’s frame the right lightning bolt occurred before t' = 0 and the left one occurred after t' = 0. So, the line t’ = 0, which is the x-axis of the train, goes under point L1, through the origin O and above the point L2. That is, The x’-axis is rotated in the opposite direction to the rotation of the ct’-axis. Let’s try to find the angle of the rotation of the x’-axis. On a plane, a light pulse expends so that it forms a circle that grows with time. In three dimensional time-space it forms a cone. This is called the light cone. On two dimensional time-space, what is left from the light cone are two lines that represents the advance of light along the space line in the positive and the negative directions. For light moving in the direction x, ct = x and for light moving in the direction –x, ct = -x. So lines that describe the advance of a light pulse in space-time have a slope of ±45˚. Since light speed is the same at every reference frame, this is also true for the x', ct' coordinate system. Light pulse that starts at the origin and moves in the x direction goes through the point x=1, ct=1, and also through x'=1, ct'=1. Light pulse that starts at x'=1, ct'=0 and moves in the –x direction has a slope of -45˚ and goes through the point x'=0, ct'=1. So, the quadrangle (x'=0,ct'=0), (x'=1,ct'=0), (x'=1,ct'=1), (x'=0,ct'=1) is a rhombus, and the x'-axis and the ct'-axis form the same angle with the 45˚ line (Figure 5).
How does the grid of the coordinate system x’,ct’ look on coordinate system x,ct? All the time lines (x’=constant) will be parallel to the ct’-axis because every point on the train moves at the same speed. All space lines (ct’=constant) will be parallel to the x’-axis. We know that one unit of time in the train’s frame looks longer in Earth frame, so the distance between grid lines of x’,ct’ coordinate system in ct' direction, is greater than one. By symmetry also the distance between grid lines in the x' direction is greater (Figure 6). Exactly by how much? At this point we will leave geometry for a while and look at some equations.
The equations for transformation of events between two time-space coordinate systems were developed by Hendryc Lorentz and published about a year before Einstein published his first work on relativity. Here is one way to get to these equations that are known as Lorentz Transformation. First let’s find the factor of the time dilation. We will designate this factor with the letter γ. Going back to the light clock from the time dilation section we have the following triangle ABC:
The length of BC is l which is the distance between the two mirrors. l = ct’ where t’ is the time it takes light to go from one mirror to the other in the clock’s frame. t is the time it takes light to make the longer distance AC between the mirrors as measured from the “static” frame. By our definition t = γt’. The length of AC equals ct = γct’ = γl. The length of AB equals to the distance the clock frame moves during the time t and is
If we choose l = 1 we get:
BC = 1 AC = γ AB = γβ
We use Pythagoras’ theorem and get:
Now, if we assume that the tranformation is linear, it must be of the form:
ct = act’ + bx’ (3.1)
x = dx’ + ect’ (3.2)
Where a, b, d and e are constants for a pair of frames. We know that for a light pulse moving in the direction x we have x = ct and x’ = ct’ so for event on this line we get:
act’ + bx’ = dx’ + ect’ ax’ + bx’ = dx’ + ex’
a + b = d + e (4)
For light pulse moving in the direction –x we have x = -ct and x’ = -ct’ so
act’ + bx’ = -dx’ – ect’ act’ – bct’ = dct’ – ect’
a – b = d – e (5)
By adding (5) to (4) we get
2a = 2d a = d (6)
By subtracting (5) from (4) we get
2b = 2e b = e (7)
The line x' = 0 goes through the common origin of the two frames, and thus, for this line, when t' = 0 also t = 0. We have defined γ as the time dilation factor, so for this line t = γt'. Substituting x' = 0 and t = γ t' in (3.1) we get:
ct = γct' = act' a = γ (8)
For the line x' = 0 we also know that
Substituting x = βct and x' = 0 in (3.2) we get:
βct = ect' βγt' = et' e = βγ (9)
From (6),(7),(8) and (9):
a = d = γ and b = e = βγ
And substituting this in (3.1) and (3.2) we get the Lorentz transformation for two dimensional time-space:
ct = γ(ct' + βx') (10.1)
x = γ(x' + βct') (10.2)
where
While some sizes in
geometry are coordinate system dependent, others are invariant and remain
the same when measured from any coordinate system. In space, for instance,
the distance between two points is invariant. Thus, for all the coordinates
systems with a common origin the distance of a point from the origin is
invariant. From Pythagoras’ theorem the square of this distance in a two
dimensional space equals to From the Lorentz transformation we can see that for time-space
Since
So for two dimensional
time-space the value of
Mathematicians define a function called the metric that is typical to a geometry. This function satisfies the following conditions:
It takes two vectors as arguments and returns a number as a result. It is written as:
It is symmetric:
It is linear:
Its value is invariant.
The metric for Euclid (space) geometry is known as the dot product of vectors:
It is easy to see that
conditions 1 - 3 are satisfied by this function. It is a little more
complicate to show that it is invariant. But if we operate the function on
the same vector twice we get
The left side of the equation is the metric applied on vector with itself so it is invariant. So are the first and last parts of the right side. That makes also g(v1,v2) invariant.
The metric for time-space is known as the Minkowskian:
It can be shown in a way
similar to that we used for space, that this function satisfies the required
conditions. Note that when applying this function on a vector with itself we
get
Al and Bob are twins who live on planet Earth. On their 20th birthday Bob buys himself a spaceship and starts a voyage to planet Traal that is 8.66 light years away from Earth. His spaceship’s cruising speed is 0.866c and it accelerates so fast that its acceleration time and distance are negligible. When he gets to Traal he makes a U-turn and goes back to Earth. When he gets there, he finds out that he is only 30 years old but his twin Al is already 40 years old. This is clear from Al's point of view: Bob is going 10 years to Traal and 10 years back. time dilation factor for both parts of the journey is γ = 2, and thus Bob's time goes twice slower and only 10 years pass for him during the journey. But how do things look from Bob's point of view? What about symmetry and the second postulate? Doesn't Bob see Al's time pass slower as well? Well, there is no symmetry between Al and Bob here. While Al stays at the same inertial frame all the time, Bob is changing frames. First when he starts going from Earth, again when he makes the U-turn at Trall, and once again when he stops at Earth. But yet, all the way to Traal there is symmetry between the two and also all the way back. So what happens in the points of acceleration that makes such a big difference? Let's see how things look from Bob's point of view: When he finishes
accelerating after launch his time is nearly the same as Al's time. But
there is already one big difference between the two: For Bob, due to length
contraction, the distance to Traal is now only 4.33 light years
What happens during the U-turn? The distance to Earth grows while he slows down until it gets to its proper length 8.66 light years when Bob is at rest relative to Earth. Then it starts shrinking again until it gets back to 4.33 when Bob achieves his full speed (relative to Earth) again. More interesting is what happens to Earth time. Suppose we have on Traal a clock that is synchronizes with Earth clock (both planets are on the same inertial frame). We know that the event of Bob reaching Traal happens 10 years after launch in earth frame, so the clock on Traal shows this time when Bob gets there. As we saw in Bob's frame Earth clock shows 2.5 years after launch at that time. That is, Bob sees Earth clock showing 7.5 years earlier than Traal's clock. This is due to simultaneity differences. When Bob completes his U-turn he has the same speed and the same distance to Earth, but while before the U-turn Earth was moving away from him, now it moves towards him. Thus, the difference between clocks reads will be the same, but in the other direction. Traal's clock will still shows 10 years, but Earth clock shows 17.5 years. During the way back that takes 5 years in his frame, Bob sees 2.5 more years pass on Earth, so when he gets there, Earth clock shows 20 years and his own shows 10 years. In Bob's frame only 2.5 years pass on Earth during his way to Traal and 2.5 years in his way back. The remaining 15 years pass in the short time (according to his clock) in which he makes the U-turn.
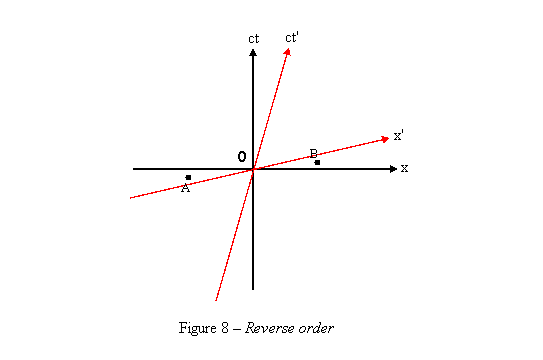
There are some arguments that show why an object or even information moving faster than light contradicts with the laws of special relativity. I shall describe one here. We distinguish between three types of lines in time-space: · A line with a slope of 1 or -1 (45°) is called a light-like line and can describe the motion of a light pulse. · A line with a slope greater than 1 or smaller than -1 is called a time-like line and can be the ct-axis of another frame. · A line with a slope greater than -1 and less than 1 is called a space-like line and can be the x-axis of another frame. A line in space-time remains the same type in any reference frame. Moving faster than light means going along a space-like line in time-space. But two events on a space-like line can happen in opposite order in two frames. In figure 8 we can see that for the black coordinate system A happens before B, but for the red coordinates system B happens before A. If we could send information about B along the space-like line connecting it to A in the red frame, this information would go back in time in the black frame, and get to A before B has happened. This leads to the paradox of action affects its own cause, like the known example of the time traveler who kills his own grandfather. Suppose Alpha and Beta are two enemy planets. Event B represents the launch of a missile from Beta that aims to destroy Alpha. A space-ship passing by notices the launch and transmits a warning message to Alpha. The message goes faster than light relative to the space-ship's frame (the red coordinates) and gets to Alpha before the launch occurred in its own (black) frame. This leaves enough time for beta to send another faster than light message to a war space-ship near Beta that in turn destroys Beta before the launch of the missile...
If an object B is moving with velocity v relative to A, and C is moving relative to B in the same direction with velocity u, what will be the relative velocity w between A and C? Obviously if we just add v and u we can exceed light speed. Both v and u can be more than 0.5c.
We can understand that w is less than v + u if we think about the fact that for A distances of B look shorter and the time of B is slower, thus A sees C passing a shorter distance in longer time than B sees. There is also a correction due to the increase of simultaneity difference with distance. Let's use Lorentz transformation to find the relation between u, v and w. If we take two points in
time-space that C pass through and sign them as
By Lorentz transformation
From (11.1)
Since
or, when substituting (11.2)
(12) is sometimes called
the relativistic velocity addition equation. But since this non linear
function is definitely not an addition, the name “velocity composition
equation” is much more suitable for it. Note that if both v and u
are very small compared to c, then
This nonlinear behavior of velocities breaks most of the laws of non-relative dynamics. Suppose we launch a missile to space. It burns all its fuel and gets a velocity v. a spaceship moving along with it, refills its tank, and it starts the engine again until all the fuel is gone. Now, relative to the spaceship, it gets the same velocity v, but relative to us it has less than 2v. We can see that neither Newton's second law F = ma, nor energy conservation as we know it are valid anymore. We had the same force and the same fuel energy in both parts of the journey of the missile, but, relative to us, the velocity after the second part is less than twice the velocity after the first part. Thus, it had less acceleration, and gained less kinetic energy in the second part. Let's now look at the following situation: Two balls of the same mass m are moving in opposite directions at the same speed v relative to an inertial frame S (Figure 10a). They collide, stick to each other and come to rest. Relative to S, the non-relative total momentum Mv of the balls before the collision is mv-mv=0 and is 2mv.0 after the collision. So, relative to S the momentum is conserved. But what do we see if we look at the same collision from a frame S' that is moving with speed v relative to S? Before the collision one of the balls is at rest and the other is moving at a speed w that is less than 2v. So, the momentum before the collision is less then 2mv. After the collision, the balls stuck together move at v since they are at rest relative to S. So, the momentum is 2v. The momentum is not conserved relative to S'.
We saw that three of the most important laws of dynamics - the conservation of energy, the conservation of momentum and the second law of Newton - fail with relativity. New laws must be found and they have to fulfill the following conditions: · They must be mathematically correct, and comply with the Lorentz transformation. · They must reduce to the known non-relativistic laws when v << c. · They must be proved correct when tested by experiments.
Most problematic is the conservation of energy. It appears that separate conservation of mass and energy is not possible when it comes to relativity. Einstein presented the following scenario: In a stationary closed box, a photon leaves the internal face of the left wall and is absorbed in the right wall. It was known before Einstein that light, though it has no mass, has momentum and can move objects. So, when the photon leaves the left wall of the box it pushes the box slightly to the left. The motion of the box stops shortly later as the photon hits the right wall, but the box is now shifted slightly to the left. Physics tells us that the center of mass of a closed system cannot be changed without an external force, so the photon must have carried a tiny amount of mass from the left wall to the right. Einstein concluded that mass and energy are equivalent and exchangeable. His famous equation shows the internal energy stored in a body at rest:
The total energy of a moving body is the sum of the internal energy and the kinetic energy and is given by the formula:
Where γ is calculated using the velocity of the body. This total energy is conserved in a closed system relative to any reference frame. The kinetic energy is thus given by:
This formula is a little problematic, for it does not reduce to the non-relativistic form when v << c and γ ≈ 1. Instead, we get K ≈ 0. This happens because when speeds are low, the kinetic energy is very small relative to the internal energy. It makes this formula useless when we deal with kinetic energy of low speeds. A latest work called “Millennium Relativity” suggests a new expression for the kinetic energy:
This equation is just
another form of Einstein’s equation (15) and can be directly derived from it
(you can look here). But this form of the
equation does reduce to the non-relativistic formula
Momentum
The relativistic momentum is defined by the expression:
This value is also conserved for a closed system relative to any reference frame. Note that with inelastic collisions the mass is not necessarily conserved. Some or all of the kinetic energy that is lost in the collision might transform into mass. So, when we calculate momentum before and after an inelastic collision we must use a different mass in the momentum expression.
Force and acceleration
Instead of Newton’s second law, special relativity defines the relationship:
We can see that for low velocities it becomes F = m(dv/dt) = ma. We must note that γ is also changed with velocity and that force may be different when measured from different reference frames. Thus, force is not a very useful concept in relativity.
Relativistic Mass
We can see that the expression γm appears in all the dynamic formulas. This expression is sometimes called the relativistic mass. We define the rest mass M0 of an object as the mass measured in its own reference frame, and say that the mass of an object increases with velocity so that M = γM0. M0 is what we referred to as the mass m. With this definition the expression for momentum retains the non-relativistic form p = Mv and the total energy becomes E = Mc2 for all reference frames. There are two arguments against this approach. First, it is preferred to look at mass as a property of an object that is independent from the reference frame. Second, one of the reasoning for the definition of relativistic mass was trying to keep Newton’s second law in its original form. But this requires a definition of a different mass for an object in the direction of its motion and perpendicular to it, because it is harder to accelerate an object in the direction of its motion than perpendicular to it.
With the 4-vector approach all the physical entities are defined as four dimensional vectors. Examples are 4-velocity, 4-force, 4-acceleration and 4-momentum (energy is one of the components of the 4-momentum). All the vectors are defined so that they are transformed with Lorentz transformation in the same way that events in space-time do. If a vector is defined by its components so that V = (x0, x1, x2, x3), the value of
|