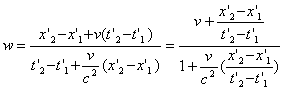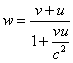עברית

אנגלית

דף הבית

 

להבין את תורת היחסות הפרטית

תוכן העינינים

 

 

 

להבין את תורת היחסות הפרטית

מאת רפי מור

2004

 

 

מטרת המאמר הזה היא להציג את תורת היחסות הפרטית באופן פשוט להבנה. המאמר סוקר את הנושאים הבסיסיים בתורת היחסות הפרטית באופן לא פורמלי וללא שימוש במתמטיקה גבוהה כך שכל אחד שיש לו ידע בסיסי בפיזיקה יוכל להבין.

 

 

רקע

 

כאשר התגלו במאה ה-18 התכונות הגליות של האור (ושל קרינות אלקטרומגנטיות אחרות), הניחו המדענים שצריך להיות חומר כלשהו שבו נעים הגלים. הם האמינו שחומר כזה ממלא את כל החלל וקראו לו אתר.

ב-1887 אלברט מיקלסון ואדוארד מורלי ביצעו ניסוי שבו ניסו להראות את התנועה של כדור הארץ ביחס לאתר על ידי מדידת שינויים במהירות האור בכיוונים שונים. לתדהמתם הרבה, הם לא מצאו כל שינוי במהירות האור ללא תלות בתנועת הארץ יחסית למקור האור או יחסית לאתר.

בעקבות תוצאות הניסוי הזה שידוע בשם ניסוי מיקלסון-מורלי, נטשו רוב הפיזיקאים את התיאוריה בדבר קיום האתר. בהעדר האתר אין גם מערכת יחוס מוחלטת שבאמצעותה ניתן לקבוע מה נמצא בתנועה בחלל ומה במנוחה.

זאת הייתה נקודת המוצא שבה החל אינשטיין את עבודתו על תורת היחסות.

 

שתי הנחות הייסוד

 

אינשטיין ביסס את תורתו על שתי הנחות יסוד:

 

1.       עקרון היחסות:

חוקי הפיזיקה זהים בכל מערכות הייחוס האינרטיות.

 

2.       אחידות מהירות האור:

למהירות האור בריק יש ערך קבוע c בכל מערכת ייחוס אינרטית.

 

הנחת היסוד הראשונה קובעת סימטריה או שוויון בין כל מערכות הייחוס האינרטיות (שאינן בתאוצה). אפשר להניח לגבי כל מערכת ייחוס אינרטית שהיא נמצאת במנוחה בעוד ששאר המערכות האינרטיות נעות במהירות קבועה לאורך קווים ישרים. נקודה חשובה נוספת בהקשר לכך היא, שבהעדר מערכת ייחוס מוחלטת אין גם הגדרה מוחלטת של מקום או נקודה בחלל. מה שהוא נקודה קבועה בחלל לגבי מערכת אחת, הוא נקודה נעה עבור מערכת אחרת. אנשים שנמצאים בשתי מערכות שנעות זו ביחס לזו לא יוכלו להסכים על המקום שבו קרה אירוע בעבר.

הנחת היסוד השנייה היא זו שמאלצת אותנו לשנות את חוקי הפיזיקה כפי שהכרנו אותם לפני תורת היחסות. תארו לעצמכם שתי ספינות חלל שחולפות זו ליד זו, אחת פונה אל השמש והשנייה ממנה והלאה. שתיהן צופות בפוטון אחד שבא מהשמש. ללא יחסות יראו שתי הספינות את הפוטון לאחר שנייה אחת במרחק שניית אור אחת מהן. אלא שבינתיים הספינות התרחקו זו מזו ולכן יראו את הפוטון בשני מקומות שונים באותו הזמן.

כדי לראות איך ניתן ליישב את הבעיה הזאת ניקח דוגמה שנתן אינשטיין עצמו.

 

יחסיות הסימולטניות

 

רכבת נוסעת במהירות קבועה לאורך מסילה ישרה. אישה עומדת בדיוק באמצע הרכבת וגבר עומד מחוץ לרכבת סמוך לפסים. התרחיש הבא מתואר כפי שהוא נראה או נמדד או בעצם כפי שהוא קורה באמת מנקודת מבטו של הגבר:

כאשר האישה שברכבת נמצאת בדיוק מולו, שני ברקים פוגעים בשני הקצוות של הרכבת. הם משאירים סימנים גם על הרכבת וגם על המסילה במקומות שבהם פגעו. האור מהברקים מתחיל להתפשט במהירות קבועה לכל הכוונים כמתואר בתרשים 1א'. שבריר של שנייה מאוחר יותר מגיע האור הבא מקדמת הרכבת אל האישה כפי שנראה בתרשים 1ב'. קצת אחר-כך האור משני הברקים מגיע אל האיש שמחוץ לרכבת בו זמנית כפי שנראה בתרשים 1ג'. לבסוף מגיע האור מהברק שפגע בקצה האחורי של הרכבת אל האישה.

 

 

 

 

 

המשפטים הבאים נכונים במערכת הייחוס של הגבר:

 

א.      האישה נמצאת במרכז הרכבת.

ב.      שני הברקים התרחשו בו זמנית.

ג.        מהירות התקדמות האור משני הברקים שווה.

ד.      האור מהברק הקדמי מגיע אל האישה לפני האור מהברק האחורי.

 

עכשיו ננסה לראות איך נראים הדברים מנקודת מבטה של האישה. אנחנו כבר יודעים על הבדל אחד בין שתי מערכות הייחוס: במערכת הייחוס של הגבר המקומות שבהם מתרחשים הברקים הם הנקודות על המסילה שבהן הם השאירו סימנים. במערכת הייחוס של האישה הנקודות הן בקצוות של הרכבת. מכאן שבמערכת הייחוס שלה האישה נמצאת במרחק שווה משני האירועים כל הזמן. אם נניח שכל המשפטים למעלה נכונים גם במערכת של האישה, תהיה כאן סתירה לוגית: האור לא יכול לנוע מרחקים שווים במהירות שווה ועם זאת לא להגיע באותו זמן. לכן, לפחות אחד מהמשפטים (וזה יכול להיות כל אחד מהם) איננו נכון במערכת הייחוס של האישה.

לו היינו מדברים על שתי פיסות מתכת שניתזו מפגיעת הברק ולא על אור, היה זה משפט ג' שלא היה נכון במערכת הייחוס של האישה. אם מהירותן של שתי פיסות המתכת שווה ל-v במערכת הייחוס של הגבר, במערכת הייחוס של האישה מהירות הפיסה שבאה מלפנים תהיה v+V ומהירות הפיסה שבאה מאחור תהיה v-V, כאשר V היא מהירות הרכבת. אבל על פי הנחת היסוד מספר 2 אין זה המקרה כאשר אנו מדברים על אור. מהירות האור נשארת קבועה בכל מערכת ייחוס. לכן, אחד מהמשפטים האחרים צריך להיות זה שאיננו נכון במערכת הייחוס של האישה.

נניח שזהו משפט ד'. כלומר, למרות שהאיש רואה את האור מהברק הקדמי מגיע אל האישה לפני האור מהברק האחורי, האישה רואה את האור משני הברקים מגיע בו זמנית. הנחה כזאת יכולה להביא לתוצאות מוזרות ביותר: נניח שאנו מניחים שני תאים פוטו-אלקטריים על הרכבת בנקודה P שבה נפגש האור משני הברקים לפי מערכת הייחוס של הגבר. אחד התאים מופנה קדימה והשני לאחור. את התאים מחברים לנפץ של פצצה, כך שאם שני התאים מוארים בו-זמנית הפצצה מתפוצצת. במערכת הייחוס של הגבר הפצצה תתפוצץ מכיוון שהאור יגיע לשני התאים בו-זמנית. במערכת הייחוס של האישה הפצצה לא תתפוצץ מכיוון שבמערכת שלה ההבזקים מהברקים נפגשים על-ידה ולא בנקודה P. יהיה קשה מאד להסתדר עם ההבדל הזה בין המערכות. יש לזכור שקל מאד לעבור ממערכת ייחוס אחת לשנייה. כל מה שדרוש הוא קצת תאוצה. תארו לעצמכם שהאיש יושב למחרת היום בבאר כשפתאום נכנסת האישה. "איך ייתכן שאת כאן בחיים?" ישאל הגבר מופתע. "ראיתי את הרכבת שלך מתרסקת לרסיסים אתמול ולא היו כל ניצולים." "על מה אתה מדבר?" שואלת האישה. "הרכבת הגיעה בשלום לתחנה הסופית שבה גם ירדתי ממנה."

אפשר לראות שפתרון שגורר מצב חומרי שונה בשתי מערכות ייחוס איננו מתקבל על הדעת.

אפשר להראות בעיה דומה אם אנחנו מנסים לפתור את הסתירה על-ידי הנחה שמשפט א' אינו נכון במערכת הייחוס של האישה, ולמרות שהגבר מודד מרחקים שוים בין האישה לשני הקצוות של הרכבת, האישה רואה את עצמה קרובה יותר לקצה הקדמי של הרכבת מאשר לקצה האחורי. נניח שעל רצפת הרכבת מונח מקל ארוך מאוד שמגיע מהאישה עד לקצה הקדמי של הרכבת. האישה מרימה את המקל ומנסה ללחוץ בעזרתו על בלם החירום שבקצה האחורי של הרכבת. במערכת הייחוס שלה היא לא תצליח כי המקל יהיה קצר מדי ולכן הרכבת תמשיך לנסוע. במערכת הייחוס של הגבר היא תצליח והרכבת תעצור.

נשארנו עם משפט ב'. לא נותר לנו אלא להניח שבמערכת הייחוס של האישה הברק הקדמי מתרחש לפני הברק האחורי. הבעיה היחידה בפתרון הזה היא שהוא נשמע מאד מוזר. אנחנו רגילים לחשוב על הזמן כעל דבר מוחלט ולא תלוי במערכת ייחוס. מה שקורה עכשיו קורה עכשיו ולא משנה מאיפה אתה מסתכל על זה. אבל בואו לא נשכח כמה מוזר זה נשמע כשמספרים לנו בפעם הראשונה שכדור הארץ הוא עגול ואי שם רחוק מתחתנו עומדים אנשים כשרגליהם פונות אלינו וקוראים לכיוון שפונה אלינו "למטה". בחלק הקטן של פני כדור הארץ שאנו מכסים בחיי היומיום העקמומיות היא כל כך קטנה שאפשר להניח שהוא שטוח. באותו אופן, במהירויות הקטנות שאנחנו פוגשים בחיי היומיום אפשר להניח שהזמן הוא מוחלט אבל כשמדברים על מהירויות גבוהות יותר רואים שאין הדבר כך.

מצאנו עכשיו את אחד החוקים של תורת היחסות – יחסיות הסימולטניות. שני אירועים שקורים בו-זמנית במערכת ייחוס אחת מתרחשים בהפרשי זמן במערכת אחרת. שני שעונים שמתואמים במערכת אחת יראו הפרשי זמן במערכת ייחוס אחרת. אפשר לראות מתוך הדוגמה שלמעלה שההפרש הזה גדל עם הגדלת המהירות היחסית בין שתי מערכות הייחוס וגם עם הגדלת המרחק בין שני האירועים בכיוון התנועה היחסית של המערכות.

עכשיו עלינו לראות מה עוד שונה בין מערכות ייחוס שונות.

 

 

 

הצטמצמות האורך

 

תארו לעצמכם שני אנשים על רציף של נמל שמנסים למדוד את אורכה של אוניה השטה לאורך הרציף. אחד מהם הולך על יד החרטום והשני ליד הירכתיים. כאשר אחד מהם שורק, מסמנים שניהם על הרציף בגיר את מיקום הקצה הקדמי והאחורי של הספינה ולאחר מכן הם מודדים את המרחק בין הסימנים. השיטה פועלת כראוי. אבל מה קורה כשאדם אחד מנסה לעשות כך לבדו? הוא מסמן קצה אחד של הספינה, רץ לקצה השני ומסמן גם אותו. אבל בגלל שהספינה המשיכה לנוע בזמן שהוא רץ, תוצאת המדידה שהוא יקבל תהיה גדולה או קטנה מאורכה האמיתי של הספינה, תלוי בקצה שממנו התחיל. כדי לדעת את אורכו של דבר מה עלינו לדעת איפה נמצאים שני קצותיו בו-זמנית. אבל מה אם המושג בו-זמנית הוא יחסי? כנראה שנמדוד אורכים שונים ממערכות יחוס שונות.

 נחזור רגע למקרה הרכבת. הגבר רואה את שני הברקים פוגעים בו זמנית בשני הקצוות של הרכבת. הברקים משאירים סימנים על המסילה. עבורו, המרחק בין הסימנים שווה לאורך הרכבת. האישה, במערכת הייחוס שלה, רואה את המסילה נעה לכיוון הצד השמאלי של התרשים. הברק בימין התרשים מתרחש במערכת הייחוס הזאת ראשון ומסמן את מיקום הקצה הקדמי של הרכבת על המסילה. הברק בשמאל התרשים מסמן את הקצה האחורי של הרכבת קצת אחרי כן. בזמן שעבר בין שני הברקים נעה המסילה שמאלה עם הסימן הימני שעליה. לכן, במערכת הייחוס של האישה המרחק בין הסימנים על המסילה קטן מאורך הרכבת.

מה נמדוד אם הרכבת והמסילה יהיו באותה מערכת ייחוס, כלומר נעצור אם נעצור את הרכבת על יד הסימנים? אורך של אובייקט כפי שהוא נמדד במערכת הייחוס של עצמו נקרא האורך הנכון (proper length).  נניח שהאורך הנכון של הרכבת שווה לאורך הנכון של המרחק בין הסימנים על המסילה. זה מפר את הסימטריה הנדרשת על פי הנחת היסוד מס' 1: במערכת הייחוס של הגבר האורך הנמדד של הרכבת שווה לאורכה הנכון. במערכת הייחוס של האישה לעומת זאת, המרחק בין הסימנים קטן מהמרחק הנכון. מה אם האורך הנכון של הרכבת קטן מהמרחק הנכון בין הסימנים? הגבר רואה את הרכבת ארוכה מאורכה הנכון, בעוד שהאישה רואה את המרחק בין הסימנים קצר מהמרחק הנכון. שוב אין סימטריה. האפשרות היחידה שבה נשמרת הסימטריה היא שהאורך הנכון של הרכבת גדול מהמרחק הנכון בין הסימנים ושניהם רואים את האורכים במערכת הייחוס השנייה קצרים מאורכם הנכון. זהו עוד חוק של תורת היחסות – הצטמצמות האורך. כאשר מודדים אורכים במערכת שנעה יחסית אלינו האורכים בכיוון התנועה היחסית יהיו קצרים מאורכם הנכון.

 

 

התרחבות הזמן

 

בוא נבנה שעון אור. נשים שתי מראות עם החזרה מושלמת זו מול זו במרחק של מיקרו-שניית אור אחת בדיוק. נשלח פולס של אור כך שהוא ינוע הלוך וחזור בין שתי המראות. כל "תקתוק" של השעון יארך בדיוק מיקרו-שנייה אחת. מה נראה אם נסתכל על שעון האור ממערכת ייחוס שנעה ביחס לשעון בכיוון ניצב לתנועת האור בין המראות כפי שמתואר בתרשים 2 ? יחסית למערכת השנייה המרחק שעובר האור בין שתי המראות גדול ממיקרו-שניית אור. מכיוון שמהירות האור קבועה ייקח לאור יותר ממיקרו-שנייה לעבור את המרחק הזה. לכן בעוד שאדם שנמצא במערכת הייחוס של השעון מודד שנייה אחת בכל "תקתוק" של השעון, עבור אדם במערכת השנייה הזמן הזה ארוך יותר. במילים אחרות, האדם במערכת הייחוס השנייה רואה את הזמן במערכת של השעון עובר לאט יותר.

 

 

עקרון הסימטריה קובע שגם האיש במערכת של השעון רואה את הזמן במערכת השנייה עובר לאט יותר. זה עניין שקצת קשה לתפוס. בגלל שאנחנו כל כך רגילים לחשוב על הזמן כדבר מוחלט, קל לנו יותר לקבל ששתי מערכות רואות כל אחת את האורכים במערכת השנייה קטנים יותר, מאשר לקבל ששתי מערכות רואות כל אחת את הזמן במערכת השנייה עובר לאט יותר. עלינו להבין שלכל מערכת יש זמן נפרד משלה. זהו לא אותו הזמן שאנו מודדים ממערכות ייחוס שונות. אפשר לעשות את ההקבלה הבאה:

שני אנשים מתחילים ללכת בקו ישר מאותה נקודה בשני כיוונים שביניהם זווית α כפי שמתואר בתרשים 3 . שניהם הולכים קדימה במהירות שווה. אחרי זמן מה מסתכלים שניהם הצידה כדי לראות איפה נמצא האיש השני. שניהם רואים שיחסית לכיוון שלהם האיש השני נמצא מול נקודה על הנתיב שלהם שאותה כבר עברו, לכן שניהם מסיקים שהאיש השני נמצא מאחוריהם. זה קורה בגלל שקדימה ואחורה הם דברים שונים עבור כל אחד מהם. באותו אופן מוקדם ומאוחר הם דברים שונים עבור שני אנשים שנמצאים בתנועה יחסית ביניהם. כאשר הם מסתכלים על הזמן של האחר הם משווים אותו לזמן שלהם. כמו שכל אחד מהאנשים בתרשים רואה את השני מאחוריו, כל אחד מהאנשים במערכות הייחוס הנעות רואה את הזמן של השני עובר לאט יותר.

 

 

ראינו עכשיו את שלשת העקרונות הבסיסיים של תורת היחסות הפרטית: הצטמצמות האורך, התרחבות הזמן והיחסיות של הסימולטניות. עכשיו אנחנו צריכים את המתמטיקה של כל זה. לשם כך נציג את הרעיון של החלל-זמן.

 

חלל-זמן

 

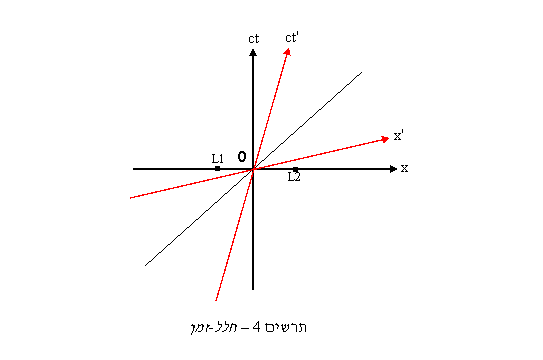
עבור כל דבר שקורה ביקום אפשר לשאול איפה הוא קרה ומתי הוא קרה. התשובה לשאלה הראשונה ממקמת את האירוע בחלל והתשובה לשנייה ממקמת אותו בזמן. כדי לקבוע את מקומו של משהו בחלל אנחנו משתמשים לרוב במערכת צירים אורתוגונלית בעלת 3 צירים ניצבים וראשית משותפת. כדי למקמם משהו בזמן דרושה לנו נקודת ייחוס בזמן והפרש הזמן בין נקודת הייחוס לאירוע שלנו.

הרעיון של מרחב-זמן מחבר את שני הדברים האלה ביחד למערכת צירים ארבע-מימדית אחת עם שלשה צירי חלל וציר זמן אחד. מיקומו של אירוע במערכת הצירים נותן את התשובות לשאלות איפה ומתי.

הרבה פעמים, כשמדובר בחלל-זמן, בוחרים יחידות מרחק וזמן כאלה שמהירות האור c שווה ל 1, כמו שנות-אור למרחק ושנים לזמן. בחירה כזאת נותנת סימטריה נוחה בגיאומטריה של החלל-זמן. הבעיה בכך היא שהדבר גורם לנוסחאות שאנו משתמשים בהן להיות תלויות בבחירת היחידות. אנחנו נשתמש בטריק שונה. במקום להראות את הזמן t על הציר הרביעי, נסמן עליו את הערכים של ct (מכפלת הזמן במהירות האור). ערך זה ייצג היטב את הזמן מכיוון שטכנית רק הכפלנו את הזמן t בקבוע, דבר שמקביל בעצם לבחירת יחידות שונות עבור הזמן. על ידי כך נשיג את הסימטריה הרצויה מבלי להפוך את הנוסחאות לתלויות בבחירת היחידות. ויש גם עוד משהו: היחידות של ct הנן בעצם יחידות אורך ואנחנו יכולים להשתמש באותן יחידות עבור כל ארבעת המימדים שלנו.

חלל-זמן ארבע-מימדי קשה מאוד להמחשה. כדי לעשות את הדברים מוחשיים יותר נשתמש רק בשני צירי חלל או אפילו אחד בלבד כדי ליצור חלל-זמן תלת או דו-מימדי. חלל-זמן דו-מימדי מספיק בשביל לתאר דברים שקורים לאורך קו ישר אחד, כמו למשל דוגמת הרכבת.

כל העניין בתורת היחסות הוא איך נראים הדברים (או איך הם באמת) ביחס למערכות ייחוס שונות. פירוש הדבר הוא בעצם טרנספורמציה של אירועים ממערכת צירי חלל-זמן אחת לשנייה. אנו יודעים איך לעשות טרנספורמציה של נקודות ממערכת צירי חלל אחת לשנייה, אבל המתמטיקה או הגיאומטריה של החלל-זמן שונה מהגיאומטריה האיוקלידית שאנו משתמשים בה עבור החלל. בואו נצייר מערכת צירי חלל-זמן דו-מימדית בעלת ציר x וציר ct כפי שמצויר בתרשים 4. נניח שאלה הם צירי החלל-זמן של האדמה בדוגמת הרכבת, כשהראשית O היא בנקודה שבה עומד האיש ובזמן שהאישה נמצאת בדיוק מולו.

 

 

הקו האדום שמסומן כ-ct' מראה את מיקומה של האישה כפי שהוא נראה מהאדמה. קו זה מתואר על ידי המשוואה:

נגדיר את β כיחס בין המהירות היחסית בין שתי מערכות הייחוס לבין מהירות האור:

 

β = v/c                                                                                                             (1)

 

במערכת הצירים של הרכבת האישה נמצאת כל הזמן בנקודה x' = 0, לכן קו זה מתאר את הציר ct' של הרכבת כפי שהוא נראה במערכת הצירים של האדמה.

אנחנו יודעים שעבור מערכת צירי חלל, אם ציר אחד של מערכת צירים מסובב בזוית α יחסית למערכת צירים אחרת, הציר השני יהיה מסובב באותה זווית ובאותו הכיוון. האם זה כך גם עבור מערכת צירי חלל-זמן?

אנחנו יודעים שבמערכת הייחוס של האדמה שני הברקים קורים בזמן t = 0. נסמן אותם בעזרת הנקודות L1 ו-L2 על מערכת הצירים. במערכת הייחוס של הרכבת הברק הימני קורה לפני t' = 0 והברק השמאלי אחרי t' = 0. לכן, הקו t' = 0 שהוא ציר ה-x של מערכת הצירים של הרכבת, עובר מתחת לנקודה L1, דרך הראשית O ומעל לנקודה L2. כלומר הציר x' מסובב בכיוון ההפוך לסיבוב של הציר ct'. בואו ננסה למצוא את זווית הסיבוב של הציר x'.

במישור, פולס של אור מתפשט באופן כזה שהוא יוצר מעגל שהולך וגדל עם הזמן. בחלל-זמן תלת-מימדי הוא יוצר קונוס שנקרא קונוס האור. בחלל-זמן דו-מימדי מה שנשאר מקונוס האור הם שני קווים אלכסוניים שמיצגים את התקדמות האור לאורך ציר החלל בכיוון החיובי ובכיוון השלילי. עבור אור שנע בכיוון x חיובי  ct = x ועבור אור שנע בכיוון x שלילי ct = -x. קווים שמתארים התקדמות של אור בחלל-זמן מיוצגים על ידי קווים בעלי שיפוע של ±45˚. כיוון שמהירות האור היא קבועה בכל מערכת יחוס הדבר נכון גם עבור מערכת הצירים  x', ct'. פולס של אור שמתחיל בראשית הצירים ונע בכיוון x עובר דרך הנקודה x=1, ct=1 וגם דרך הנקודה x'=1, ct'=1. פולס של אור שמתחיל בנקודה x'=1, ct'=0 ונע בכיוון –x שיפועו יהיה -45˚ והוא יעבור דרך הנקודה x'=0, ct'=1. מזה נובע שהמרובע

 (x'=0,ct'=0), (x'=1,ct'=0), (x'=1,ct'=1), (x'=0,ct'=1) הוא מעוין, ולכן הצירים x' ו-ct' יוצרים זווית שווה עם קו ה-45˚ (תרשים 5)

 

 

איך נראית רשת הקואורדינטות של המערכת x’,ct’ במערכת x,ct? כל קווי הזמן (x' קבוע) יהיו מקבילים לציר ct' מכיוון שכל נקודה על הרכבת נעה באותה מהירות. כמו כן כל קווי החלל (ct' קבוע) יהיו מקבילים לציר x'. ידוע לנו שיחידת זמן במערכת הייחוס של הרכבת  נראית ארוכה יותר במערכת הייחוס של הקרקע ולכן המרווח בין קווי הרשת של מערכת הקואורדינטות x’,ct’ בכיוון ct' יהיה גדול מיחידה. בשל הסימטריה גם המרווחים בכיוון x' יהיו גדולים באותה מידה. בכמה בדיוק?

בשלב הזה נעזוב לרגע את ההמחשה הגיאומטרית ונעבור לנוסחאות.

 

טרנספורמציית לורנץ

 

הנוסחאות לטרנספורמציה של אירועים בין שתי מערכות צירים בחלל-זמן פותחו על ידי הנדריק לורנץ ופורסמו כשנה לפני שאינשטיין פירסם את עבודתו הראשונה על תורת היחסות. נביא כאן דרך אחת לפיתוח המשוואות שידועות כטרנספורמציית לורנץ.

ראשית נמצא את מקדם התרחבות הזמן. נסמן אותו באות γ. נחזור לשעון האור שבסעיף התרחבות הזמן ונסמן את המשולש ABC באופן הבא:

 

 

אורך הקו BC שווה ל l שהוא המרחק בין שתי המראות. l = ct’ כאשר t’ הוא הזמן שלוקח לאור לעבור את המרחק ביו שתי המראות במערכת הייחוס של השעון. t הוא הזמן שלוקח לאור לעבור את המרחק הגדול יותר AC בין המראות כפי שהוא נמדד במערכת הייחוס ה"נייחת". עלפי ההגדרה t = γt’. ולכן אורך הקו AC שווה ct = γct’ = γl. אורך הקו AB שווה למרחק שעברה מערכת השעון בזמן t ונתונה על ידי:

 

 

אם נבחר l = 1 נקבל:

 

BC = 1   AC = γ   AB = γβ

 

נשתמש במשפט פיטגורס ונקבל:

 

                                                                                                   (2)

 

אם אנחנו מניחים שטרנפורמציה בין מערכות חלל-זמן היא לינארית משוואות הטרנספורמציה צריכות להיות מהצורה:

 

ct = act’ + bx’                                                                                                (3.1)

 

x = dx’ + ect’                                                                                                 (3.2)

 

כאשר a, b, c ו-d הנם קבועים עבור זוג מערכות ייחוס.

ידוע לנו שעבור פולס של אור שנע בכיוון x מתקיים x = ct וגם  x’ = ct’ ולכן עבור אירועים שנמצאים על הקו הזה אנחנו מקבלים:

 

act’ + bx’ = dx’ + ect’

ax’ + bx’ = dx’ + ex’

 

a + b = d + e                                                                                                  (4)

 

עבור פולס אור שנע בכיוון –x מתקיים x = -ct ו- x’ = -ct’ ולכן

 

act’ + bx’ = -dx’ – ect’

act’ – bct’ = dct’ – ect’

 

a – b = d – e                                                                                                    (5)

 

על ידי חיבור של (4) ו-(5) נקבל

 

2a = 2d

a = d                                                                                                               (6)

 

על ידי חיסור (5) מ-(4) נקבל

 

2b = 2e

b = e                                                                                                                (7)

 

הקו x' = 0 עובר דרך הראשית המשותפת של שתי מערכות הצירים ולכן עבור הקו הזה כאשר

 t' = 0 גם t = 0. הגדרנו את γ כמקדם התרחבות הזמן ומכאן שעבור הקו הזה   t = γt'.

אם נציב  x' = 0  ו- t = γ t' ב-(3.1) נקבל:

 

ct = γct' = act'

a = γ                                                                                                                (8)

 

עבור הקו x' = 0 אנחנו יודעים גם ש:

 

אם נציב  x  = βct  ו-   x' = 0ב-(3.2) נקבל:

 

βct = ect'

βγt' = et'

e = βγ                                                                                                              (9)

 

מתוך (6), (7), (8) ו-(9):

 

a = d = γ and b = e = βγ

 

ואם נציב תוצאה זו ב-(3.1) ו-(3.2) נקבל את טרנספורמצית לורנץ עבור חלל-זמן דו-מימדי:

 

 

 

ct = γ(ct' + βx')                                                                                               (10.1)

 

x = γ(x' + βct')                                                                                                (10.2)

 

כאשר:

 

            

 

המטריקה

 

בעוד שכמה גדלים בגיאומטריה תלויים במערכת הייחוס, גדלים אחרים אינם תלויים בה והם קבועים עבור כל מערכות הייחוס. בחלל למשל, המרחק בין שתי נקודות נשאר שווה בכל מערכות הייחוס. לכן, עבור כל מערכות הצירים שלהן ראשית משותפת, המרחק מנקודה כלשהי לראשית הוא בלתי משתנה. ממשפט פיטגורס אנו יודעים שהריבוע של המרחק הזה נתון על ידי  

ולכן ערכו של הביטוי הזה הוא בלתי משתנה בחלל.

מתוך טרנספורמציית לורנץ אפשר לראות שעבור החלל-זמן

 

 

 

                                        מכיוון ש מקבלים

 

 

אם כן, עבור חלל-זמן דו-מימדי הגודל  הוא בלתי משתנה.

 

מתמטיקאים מגדירים פונקציה שנקראת המטריקה והיא אופיינית לגיאומטריה מסוג מסוים. הפונקציה הזאת צריכה לקיים את התנאים הבאים:

 

1. היא מקבלת שני ווקטורים ונותנת תוצאה שהיא מספר. רושמים אותה באחת מהצורות הבאות:

 

  או

 

2. היא סימטרית:

 

 

3. היא לינארית:

 

 

4. הערך שלה הוא בלתי משתנה (אינו תלוי במערכת ייחוס)

 

המטריקה עבור גיאומטריה אויקלידית (גיאומטריה של חלל) ידועה כמכפלה הווקטורית:

 

 

קל לראות שהתנאים 1 עד 3 מתקיימים עבור הפונקציה הזאת. קצת קשה יותר לראות שהיא בלתי תלויה במערכת הצירים. אם נכניס לפונקציה את אותו הווקטור פעמיים נקבל

הראנו קודם שהגודל הזה הוא בלתי משתנה. אם נניח שהווקטור V הוא סכום של שני ווקטורים אחרים כך

 ש-  אז בעזרת חוקי הסימטריות והלינאריות אפשר להראות ש:

 

 

הצד השמאלי של המשוואה הוא הפעלה של הפונקציה על שני ווקטורים זהים ולכן הוא בלתי משתנה. כמוהו גם האיבר הראשון והאחרון בצד הימני של המשוואה. מכאן נובע שגם הגודל    הינו בלתי משתנה.

 

המטריקה של החלל-זמן ידועה כמינסקובסקיאן ונתון ע"י:

 

 

אפשר להראות בדרך דומה לזו שהשתמשנו בה עבור החלל כדי להראות שגם הפונקציה הזאת מקיימת את התנאים הדרושים. שימו לב שכאשר מפעילים את הפונקציה על שני ווקטורים זהים מקבלים את הביטוי       

 שכבר ראינו שהוא שהוא בלתי משתנה בחלל-זמן.

 

פרדוקס התאומים

 

אודי ובני הם תאומים שגרים על כדור הארץ. ביום הולדתם ה-20 קונה בני לעצמו במתנה ספינת חלל משוכללת ויוצא למסע אל כוכב הלכת טראל שנמצא במרחק 8.66 שנות אור מכדור הארץ. מהירות השיוט של ספינת החלל שלו היא 0.866c והיא מאיצה כל כך מהר שהזמן והמרחק של התאוצה זניחים. כאשר הוא מגיע לטראל הוא עושה סיבוב פרסה וחוזר לכדור הארץ. כשהוא מגיע בחזרה, הוא מגלה להפתעתו שלמרות שהוא עצמו רק בן שלושים אחיו התאום אודי כבר בן ארבעים.

זה די ברור מנקודת מבטו של אודי: בני טס 10 שנים אל טראל ו-10 שנים בחזרה. מקדם התרחבות הזמן בכל אחד משני החלקים של הדרך הוא γ = 2 ולכן הזמן אצל בני עובר פי שניים לאט יותר, כך שעל פי שעונו עוברות רק 10 שנים עד שהוא חוזר.

אבל כיצד נראים הדברים מנקודת מבטו של בני? מה עם הסימטריה? האם בני לא רואה גם הוא את הזמן אצל אודי עובר לאט יותר?

ובכן, במקרה זה אין סימטריה בין אודי לבני. בעוד שאודי נשאר כל הזמן באותה מערכת ייחוס אינרטית, בני משנה את מערכת הייחוס שלו כמה פעמים. לראשונה כשהוא עוזב את כדור הארץ, פעם נוספת כאשר הוא עושה את סיבוב הפרסה סמוך לטראל ושוב כאשר הוא עוצר בכדור הארץ. אבל עדיין ישנה סימטריה ביניהם במשך כל הדרך אל טראל וגם במשך כל הדרך חזרה. מה עם כן קורה בנקודות שבהן הוא מאיץ ומאט שגורם להבדל גדול שכזה בין השניים?

בואו ונראה איך נראים הדברים מנקודת מבטו של בני:

כאשר הוא גומר להאיץ ביציאתו מכדור הארץ הזמן אצלו כמעט זהה לזמן של אודי, אבל יש כבר הבדל גדול בין השניים: אצל בני, בגלל הצטמצמות האורך, המרחק לטראל הוא עכשיו רק 4.33 שנות אור  ( 'x = γx ). זה מקצר את הדרך שלו לטראל בחצי והוא מגיע לשם תוך חמש שנים בלבד. מכיוון שעבורו הזמן של אודי עובר פי שניים לאט, הזמן של אודי נראה לבני רק 2.5 שנים מהשיגור כאשר הוא מגיע לטראל. מה קורה במהלך סיבוב הפרסה? המרחק לכדור הארץ גדל כל זמן שהוא מאט, עד שהוא מגיע למרחק הנכון 8.66 שנות אור כאשר בני נמצא במנוחה ביחס לכדור הארץ. אז מתחיל המרחק להצטמצם שוב עד שהוא חוזר להיות 4.33 שנות אור כאשר בני מגיע שוב למהירותו המרבית (יחסית לכדור הארץ). מעניין יותר מה קורה לזמן על כדור הארץ. נניח שיש על טראל שעון שמתואם עם השעון של אודי שעל כדור הארץ. (שני כוכבי הלכת נמצאים באותה מערכת ייחוס אינרטית). אנחנו יודעים שאירוע הגעתו של בני לטראל קורה עשר שנים אחרי השיגור במערכת הייחוס של כדור הארץ ולכן השעון על טראל יראה את הזמן הזה כאשר בני מגיע לשם. כמו שראינו, השעון על כדור הארץ מראה על פי בני באותו זמן רק 2.5 שנים מהשיגור. כלומר בני רואה את השעון על כדור הארץ מפגר ב-7.5 שנים אחרי השעון בטראל. זה קורה בגלל הבדלי הסימולטניות בין שתי מערכות הייחוס. כאשר בני משלים את סיבוב הפרסה, המהירות והמרחק שלו מכדור הארץ שווים לאלה שהיו לפני סיבוב הפרסה, אבל בשעה שלפני סיבוב הפרסה כדור הארץ התרחק ממנו, כעת הוא מתקרב אליו. לכן ההבדל בין קריאות השעון הוא זהה אבל כיוונו הפוך. השעון של טראל יראה עדיין 10 שנים אחרי השיגור, אבל השעון על כדור הארץ יראה 17.5 שנים. החזרה לכדור הארץ לכדור הארץ נמשכת על פי שעונו של בני 5 שנים, ובזמן הזה הוא רואה עוד 2.5 שנים חולפות על כדור הארץ כך שכאשר הוא מגיע שעון הארץ מראה 20 שנה ושעונו מראה 10 שנים. במערכת הייחוס של בני רק 2.5 שנים עוברות על כדור הארץ במהלך הדרך לטראל ו-2.5 שנים בדרך חזרה. יתר 15 השנים עוברות על הארץ בזמן הקצר שבו הוא עושה את סיבוב הפרסה.

 

לנוע מהר מהאור?

 

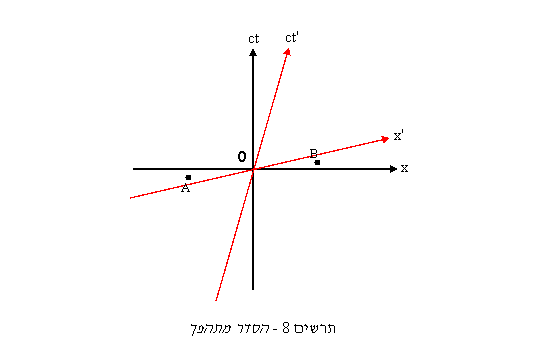
יש כמה טעונים שמראים שהאפשרות שגוף, או אפילו מידע שינוע מהר מן האור עומדת בסתירה לחוקים של תורת היחסות הפרטית. אציג אחד מהם כאן.

אנחנו מבדילים בין שלושה סוגי קוים בחלל-זמן:

·        קוים בעלי שיפוע שווה 1 (45º) נקראים קוים דמויי אור והם יכולים לתאר את תנועתו של פולס של אור.

·        קווים בעלי שיפוע גדול מ-1 או קטן מ- 1- נקראים קוים דמויי זמן והם יכולים להיות ציר ה-ct של מערכת יחוס אחרת.

·        קוים בעלי שיפוע גדול מ- 1- וקטן מ-1 נקראים דמויי חלל ויכולים להיות ציר ה-x של מערכת יחוס אחרת.

קו בחלל-זמן נשאר מאותו סוג בכל מערכת יחוס.

תנועה מהירה מן האור היא תנועה לאורך קו דמוי חלל. אבל, שני אירועים שנמצאים על קו דמוי חלל יכולים לקרות בסדר הפוך בשתי מערכות יחוס שונות. בתרשים 8 אנחנו יכולים לראות שעבור מערכת הצירים השחורה האירוע A קורה לפני האירוע B, אבל במערכת הצירים האדומה B קורה לפני A. לו יכולנו להעביר במערכת הייחוס האדומה מידע על B לאורך הקו דמוי החלל שמחבר אותו ל-A, המידע היה עובר אחורה בזמן במערכת הייחוס השחורה, ומגיע ל-A לפני ש-B קרה. זה מוביל לפרדוקס של פעולה המשפיעה על הגורם לה, כמו הדוגמה הידועה של הנוסע בזמן שהורג את סבו.

נניח שאלפא וביטא הם שני כוכבי לכת עוינים. האירוע B מיצג שיגור של טיל מביטא במטרה להשמיד את אלפא. ספינת חלל שעוברת בסמוך מזהה את השיגור ומשדרת לאלפא הודעת אזהרה. ההודעה עוברת במהירות גבוהה ממהירות האור יחסית למערכת הייחוס של ספינת החלל (האדומה) והיא מגיעה לאלפא לפני שהשיגור אירע במערכת הייחוס שלו (השחורה). זה מותיר זמן מספיק לאלפא לשלוח עוד הודעה מהירה מן האור לספינת קרב סמוכה לביטא וזו משמידה את אלפא עוד לפני ששוגר הטיל...

 

 

 

 

צירוף מהירויות

 

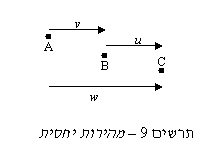
אם גוף B נע ביחס לגוף A במהירות v וגוף C נע ביחס ל-B באותו הכיוון במהירות u, מה תהיה המהירות היחסית w בין A ל-C? ברור שאם פשוט נסכם את המהירויות נוכל להגיע למהירות גדולה ממהירות האור. גם v וגם u יכולות להיות גדולות מ-0.5c.

 

 

אפשר להבין ש-w צריך להיות קטן מ- v + u אם לוקחים בחשבון שעבור A מרחקים של B נראים קצרים יותר והזמן של B נראה ארוך יותר ולכן A רואה את C עובר מרחקים קצרים יותר בזמנים ארוכים יותר מאלה שרואה B. צריך להכניס גם תיקון בשל הפרשי הסימולטניות שהולכים וגדלים עם ההתרחקות של C.

נשתמש בטרנספורמציית לורנץ כדי למצוא את היחסים בין v, u ו-w.

 אם ניקח שתי נקודות בחלל-זמן ש-C עובר דרכן ונסמן אותן ב- 

ו-  במערכת הצירים של A וב- ו- במערכת הצירים של B אנחנו יכולים לראות ש:

 

                                                                                                    (11.1)

                                                                                                    (11.2)

 

מתוך טרנספורמציית לורנץ:

 

                                                                                        (12.1)

                                                                                        (12.2)

                                                                                        (12.3)

                                                                                        (12.4)

 

מ-(11.1) נקבל:

 

 

מכיוון ש  נקבל:

 

 

ואם נציב את (11.2) נגיע ל:

 

                                                                                                      (12)

 

 

המשוואה (12) נקראת לפעמים נוסחת חיבור המהירויות היחסותית, אבל מכיוון שהמשואה הלא לינארית הזאת היא בפירוש לא פעולת חיבור השם נוסחת צירוף המהירויות נראה לי מתאים יותר. שימו לב שכאשר גם u וגם v קטנות מאד ביחס ל c,

אז .

 

דינמיקה יחסותית

 

ההתנהגות הלא לינארית הזאת של המהירויות, שוברת את רוב חוקי הדינמיקה הלא יחסותית. נניח שאנחנו משגרים טיל אל החלל. הוא שורף את כל הדלק שלו ומגיע למהירות v. חללית שנעה יחד איתו ממלאת את מיכל הדלק שלו מחדש והוא מצית מחדש את המנוע עד ששוב נגמר כל הדלק. כעת, יחסית לספינת החלל, יש לו שוב מהירות v, אבל יחסית אלינו מהירותו קטנה מ-2v. אפשר לראות שגם החוק השני של ניוטון F = ma, וגם חוק שימור האנרגיה אינם נשמרים. היו לנו אותו כוח ואותה כמות אנרגיה אצורה בדלק בשני החלקים של תאוצת הטיל, אבל יחסית אלינו, המהירות שנוספה בחלק השני קטנה מהמהירות שנוספה בחלק הראשון כך שגם התאוצה וגם תוספת האנרגיה הקינטית בחלק השני היו קטנים מאלה שבחלק הראשון.

בואו נתאר את הסיטואציה הבאה: שני כדורים בעלי אותה מסה m נעים בכיוונים הפוכים ובאותה מהירות v יחסית למערכת ייחוס S (תרשים  10א). הם מתנגשים, נדבקים אחד לשני ונעצרים. יחסית למערכת S התנע הלא יחסותי הכולל Mv של הכדורים לפני ההתנגשות שווה ל- mv - mv = 0 ואחרי התתנגשות הוא שווה ל- 2mv . 0 ולכן יחסית ל-S התנע נשמר. אבל איך יראו הדברים ממערכת ייחוס S' שנעה במהירות v יחסית ל-S? לפני ההתנגשות אחד הכדורים נמצא במנוחה והשני נע במהירות w הקטנה מ-2v. לכן התנע הכולל לפני ההתנגשות יהיה קטן מ-2mv. אחרי ההתנגשות שני הכדורים הצמודים ינועו במהירות v כיוון שהם במנוחה יחסית ל-S. התנע הכולל אחרי ההתנגשות יהיה שווה ל-2mv. התנע לא נשמר יחסית ל-S'.

ראינו ששלושה מהחשובים שבחוקי הדינמיקה – חוק שימור האנרגיה, חוק שימור התנע, והחוק השני של ניוטון בצורתם הקודמת, אינם נכונים עבור תורת היחסות. יש למצוא חוקים חדשים ועליהם לקיים את התנאים הבאים:

·        הם צריכים להיות נכונים מבחינה מתמטית ולהתאים לטרנספורמציית לורנץ.

·        עליהם להצטמצם לנוסחאות הלא יחסותיות כאשר v << c.

·        הם צריכים להתאים לתוצאות של ניסויים.

 

אנרגיה

 

הבעייתי בין החוקים הוא חוק שימור האנרגיה. מסתבר שחוקי שימור נפרדים למסה ולאנרגיה לא יכולים להתקיים כשמדברים על יחסות. אינשטיין הראה זאת בתסריט הבא: בתוך קופסה סגורה שנמצאת  במנוחה ניתק פוטון מהדופן הפנימית בצידה השמאלי ונבלע בדופן שמימין. עוד לפני אישטיין היה ידוע שלמרות שלאור אין מסה, יש לו תנע והוא יכול להניע גופים. לכן, כשהפוטון עוזב את הדופן השמאלית הוא דוחף את הקופסה מעט לשמאל. התנועה של הקופסה נבלמת זמן קצר לאחר מכן כשהפוטון פוגע בדופן הימנית של הקופסה, אבל הקופסה מוסטת עכשיו מעט שמאלה. הפיזיקה קובעת שמרכז הכובד של מערכת סגורה לא יכול להשתנות ללא כוח חיצוני, לכן הפוטון צריך היה לשאת מעט מסה מהדופן השמאלית לימנית. אינשטיין הסיק מכך שמסה ואנרגיה הם שקולים וניתנים להמרה אחד בשני. הנוסחה המפורסמת שלו מראה את האנרגיה הפנימית של גוף במנוחה:

                                                                                                         (13)

 

האנרגיה הכוללת של גוף בתנועה היא הסכום של האנרגיה הפנימית והאנרגיה הקינטית והיא נתונה על ידי הנוסחה:

 

                                                                                                       (14)

 

כאשר γ מחושבת לפי מהירות התנועה של הגוף. האנרגיה הכוללת הזאת נשמרת במערכת סגורה יחסית לכל מערכת ייחוס. האנרגיה הקינטית נתונה על ידי:

 

                                                                                             (15)

 

 

הנוסחה האחרונה היא בעייתית במקצת משום שהיא אינה מצטמצמת לנוסחה הלא יחסותית כאשר v << c שאז γ ≈ 1. במקום זאת, אנחנו מקבלים  K ≈ 0. זה קורה מפני שבמהירויות נמוכות האנרגיה הקינטית היא קטנה מאד ביחס לאנרגיה הפנימית, מה שהופך את הנוסחה הזאת ללא שימושית כשמדובר במהירויות נמוכות. עבודה שנעשתה לאחרונה ונקראת "תורת היחסות של המילניום" מציעה ביטוי חדש עבור האנרגיה הקינטית:

 

                                                                               (16)

 

הנוסחה הזאת אינה אלא צורה אחרת של המשוואה של אינשטיין (15) ואפשר לגזור אותה ישירות ממנה (ראה כאן ). אבל צורה זו של המשוואה כן מצטמצמת לנוסחה הלא יחסותית  כאשר v << c וניתן להשתמש בה עבור כל טווח המהירויות.

 

תנע

 

התנע היחסותי מוגדר על ידי הביטוי:

 

                                                                                                       (17)

 

גם הביטוי הזה נשמר במערכת סגורה ביחס לכל מערכת ייחוס. יש לשים לב שבהתנגשויות שאינן אלסטיות המסה הכוללת לא בהכרח נשמרת. חלק או כל האנרגיה הקינטית שהולכת לאיבוד בהתנגשות יכולה להפוך למסה. לכן כשמציבים את המסה בנוסחת התנע צריך להשתמש במסה שונה לפני ואחרי ההתנגשות.

 

כוח ותאוצה

 

במקום החוק השני של ניוטון משתמשים בתורת היחסות הפרטית בקשרים הבאים:

 

 

אפשר לראות שעבור מהירויות נמוכות הנוסחה הופכת ל- F = m(dv/dt) = ma. צריך להבין ש- γ גם היא משתנה עם שינוי המהירות ושהכוח יכול להיות שונה במערכות ייחוס שונות. לכן, כוח הוא לא מושג שימושי כל כך ביחסות.

 

מסה יחסית

 

אפשר לראות שהביטוי γm מופיע בכל נוסחאות הדינמיקה שהראנו. לעיתים קוראים לגודל הזה המסה היחסית. מגדירים את מסת המנוחה של גוף M0 כמסה כפי שהיא נמדדת במערכת הייחוס של עצמו, ואומרים שהמסה של גוף גדלה עם מהירותו כך ש- M = γM0. הגודל M0 הוא אותו גודל שלו קראנו המסה m של הגוף. כשמשתמשים בהגדרה הזו הביטוי של התנע נשאר בצורתו הלא יחסותית p = Mv והאנרגיה הכוללת של הגוף הופכת E = Mc2 עבור כל מערכות הייחוס.

ישנם שני טיעונים נגד השימוש במושג מסה יחסית. ראשית עדיף לראות את המסה כתכונה של גוף שאינה תלויה במערכת ייחוס. שנית, אחת הסיבות לשימוש במושג זה הייתה לנסות לשמר את החוק השני של ניוטון בצורתו הלא יחסותית. אבל דבר כזה מצריך הגדרה של ערכים שונים למסה של גוף בכיוון התנועה שלו ובניצב לו, כיוון שקל יותר להאיץ גוף בניצב לכיוון התנועה שלו מאשר בכיוון התנועה.

 

גישת ה-4-ווקטור

 

גישת ה-4-ווקטור (four vector) מגדירה כל אחד מהגדלים הפיזיקליים כווקטור ארבע מימדי. דוגמאות לכך הן 4-מהירות, 4-כוח, 4-תאוצה ו-4-תנע ( האנרגיה היא אחד הרכיבים של ה-4-תנע). כל הווקטורים מוגדרים כך שהם עוברים בטרנספורמציית לורנץ באותה הצורה שבה עוברים אירועים בחלל-זמן. אם ווקטור מוגדר על ידי הרכיבים שלו כך ש- V = (x0, x1, x2, x3),

 הגודל   הוא בלתי משתנה בין מערכות ייחוס. השורש של הביטוי הזה נקרא ה"אורך" של ה-4-ווקטור. חוקי הפיזיקה מוגדרים על ידי גדלים אלה ומשתמשים באלגברת מטריצות כדי לחשב אותם.