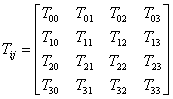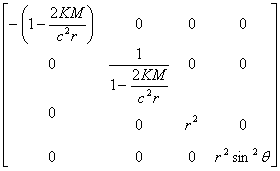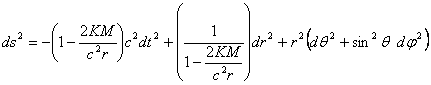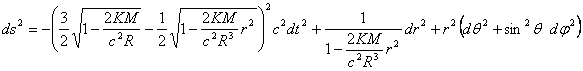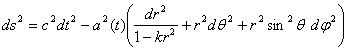|
The Field Equation and More
As was mentioned in the first part of this article, Einstein's field equation is an equation that relates the presence of matter and energy to the curvature of space-time. On the left side of the equation we have a tensor that represents the time-space curvature. This is not the whole Riemann tensor but a tensor that only describe the Ricci curvature. To make the equation look simpler, it is not the Ricci tensor itself but a new tensor that is called Einstein tensor. This tensor is built from Ricci tensor and the metric by the following formula:
Where Gij is a component of Einstein tensor, Rij is a component of Ricci tensor, R is Ricci scalar and gij is a component of the metric.
On the right side of the field equation there is another tensor that represents the matter and energy that are present at a point. We remember from Special Relativity the equivalence of the two. This tensor is called the stress-energy tensor and is signed by the letter T. The stress-energy tensor is usually defined by terms of the 4-momentum. Since the meaning of 4-vectors is not always clear and expressions like "the flow of energy in time direction" can be puzzling, I will try to use more familiar terms. Like Ricci tensor the stress-energy tensor is a rank (0,2) tensor and it is represented by a 4x4 diagonally symmetric matrix:
Without the first row and the first column we have a 3x3 matrix known as the stress tensor. Every element of it is the stress (force per unit of area) in the direction i, that acts on a surface normal to the direction j. If directions 1, 2 and 3 are x, y and z respectively, then if we take a small surface in the xy plane, T13 is the stress acting on it in the direction x and T33 is the stress acting on it in the direction z. The components in the diagonal of the matrix are normal stresses like pressure or tension. The rest of the elements are shear stresses. In GR we often speak of a "perfect fluid". This means a material that does not resist shear or tension forces like gas or liquid with no viscosity. In perfect fluid the components off the diagonal are zeros and the components in the diagonal are all positive, identical and equal to the pressure at the point. The component T00 is the energy density, that is, the energy per volume unit at the point. The components T01, T02, T03 are the density of the momentum in the direction j. T01 for example is the momentum in the direction x per volume unit. The components T10, T20, T30 tell us how much energy flows through a surface normal to i per area unit per time unit. When the only energy at a point is matter at rest all the components in the top row and the left column but T00 are zeros.
Now we have all the tensors we need and we can write the field equation:
where K is Newton's gravitational constant. The equation relates every component of Einstein's tensor to the corresponding component of the stress-energy tensor. Since both matrixes are diagonally symmetric, there are 10 different equations hiding in this tensor equation. So far we were talking about the tensors at a given point. But we might want to know the relations at every point (event) in a range of space-time. For this we shell need to know each component of the tensor as a function of the coordinates (a tensor field). Since our time-space is curved these functions are partial differential equation and we end up with 10 partial differential equations. The stress-energy tensor on the right side of the equation holds all the information about the distribution of energy and mass in space-time, but Einstein tensor on the left, has only information about Ricci curvature which is only part of the picture. The field equation only tells us how the curvature at a point is affected by the matter and energy that are present at this point. It affects only Ricci curvature. Weyl curvature at a point is caused by matter and energy at other points. The field equation tells us nothing about Weyl curvature. For calculation of Weyl curvature we need some other equations based only on the geometry and also knowledge about the curvature in the neighborhood of the points that cause this curvature. In empty space for instance, there is no matter and energy (we don't count gravitation field as energy here). The only curvature (gravity) in empty space is caused by remote bodies. The only thing the field equation can tell us about empty space is that the Ricci curvature there is 0.
An exact solution of Einstein's equation is a formula for the metric at all the points (events) in time-space, which satisfies the field equation for a known physical case. The first exact solution was the point-mass solution that was found by Karl Schwarzschild a short time after the publication of the theory of General Relativity. It solves a hypothetical case of mass that is concentrated at a point in an empty space. The solution is based on the following facts:
The spatial part of time-space in this case is spherically symmetric.
The case is static. Nothing changes along the time axis.
Einstein tensor is all zeros at any point except the one where the mass is.
Because of the spherical symmetry it would be a good idea to use spherical coordinates for space so that our time-space coordinates (0, 1, 2, 3) will be (t, r, θ, φ) where t is the time, r is the radius of a sphere around the point-mass and θ and φ are two angles similar to the longitude and latitude of Earth. Note that since space is curved, the radius r is not equal to the distance from the point mass to a point on a sphere with that radius, just as the radius of a latitude circle is not equal to the distance from the pole to a point on it. Based on the three conditions above one can show that the tensor field of the metric is given by:
K is the gravitation constant and M is the mass. If we want to know the time-space distance between two very close events, we can represent it by a tiny vector ds = (cdt, dr, dθ, dφ). We feed these coordinates to the metric twice and get:
This type of equation is called the line element equation. It turns out that the point-mass solution is also correct for a static spherical body like a star for all the points exterior to the star.
A second solution given by Schwarzschild was an approximation to the metric inside a star. Schwarzschild assumed a static spherical body made of incompressible perfect fluid. This case is also spherically symmetric and static but its stress-energy tensor is nonzero. It has nonzero pressure and density at every point inside the star. The density is constant at all the space inside the star (this is what incompressible means) and the pressure is only a function of the radial coordinate r. The line element equation for this metric is:
for r ≤ R , where R is the radius of the star.
We can see that if we substitute r = R in (2) and in (3) we get the same result, so that there is continuity between the interior and the exterior solutions.
The expression (2KM / c2) appears a few times in both the interior and the exterior metric. This expression has units of length, it is called Schwarzschild radius and is signed by rs. Schwarzschild noticed that there is a singularity of his point-mass equation when r = rs. ds gets infinite at this radius. Schwarzschild assumed that this singularity is avoided in nature by the fact that the radius of the star is always greater than this radius. This is true for regular stars and planets. Schwarzschild radius of the Sun is about 3 Km while its radius is 700,000 Km. Schwarzschild radius of the Earth is about 1 cm only. Later it has been shown that this singularity is only a coordinate singularity and not a physical singularity. Coordinates singularity is what happens in the Earths poles. There is nothing geometrically special in the poles, but there is a singularity there when we use the altitude-latitude spherical coordinate system. What happens if a star does become so dense that its radius is smaller then Schwarzschild radius? Let's look at the exterior solution first. Though the equation can't be used for a radius equals to Schwarzschild radius, it can be used for smaller radii. The equation shows strange things about space-time inside a sphere of Schwarzschild radius. Any geodesic inside this sphere that goes up towards the surface of it is a space-like line. We know from Special Relativity that nothing can go along a space-like line, not even information. This means that no matter, light or information can exit from this sphere. Moreover, no orbit around the star is possible inside the sphere. Everything inside it must constantly fall down. Even stranger is what the interior solution tells us. In normal star gravity is balanced by pressure. The star reaches a steady state in which at every point the pressure pushes matter outwards at exactly the amount needed to resist gravity at this point. In a star with a radius smaller than Schwarzschild radius, such balance is not possible. As we have seen above, pressure is part of the stress-energy tensor and contributes to gravity. Pressure, thus, has two contrasting effects: It pushes matter outwards and it causes gravity that pulls matter inwards. It turns out that for very dense stars, no matter what the pressure is, it would never be enough to balance gravity. As a result of it, the star will continuously collapse inwards until all its mass is concentrated in one dimensionless point. This point is a physical singularity. This phenomenon is called a black hole. It has been theoretically predicted that stars that remain heavier than 3 times the mass of the Sun at the end of their life will form black holes. There are also some evidences for the existence of black holes in the universe. For black holes Schwarzschild radius is also called "the event horizon". At the event horizon gravitational time dilation goes to infinity and time stops for a distant observe. Also, nothing inside the event horizon can be observed by an observer outside it.
General Relativity can be also used to form a model of the entire universe. At a very big scale we can ignore local differences in the density of the matter in space like galaxies and star systems, and think of all the matter in the universe as a perfect fluid. We do just the same when we ignore the fact that water is made of molecules and atomic particles and think of it as homogenous fluid. Models of the universe are based on two assumptions: · The universe is homogenous – everything is the same at every point of the universe. · The universe is isotropic – everything looks the same in all directions at every point of the universe. These assumptions seem to be true for the observable universe, but we have no way to know whether they are really true for the entire universe. The density of the matter in the universe can change with time. The universe can expand or contract. Homogeneity and isotropy ensure spherical symmetry at every point, so we can choose any point as the origin and use the known spherical coordinates. The metric for such universe is called Friedmann-Lemaitre-Robertson-Walker (FLRW) metric and its line element formula is:
There are two unfamiliar variables in this equation: a(t) is called the scale factor and represents the expansion of the universe as a function of time. k is used to combine three types of possible geometries of the universe into one equation. It can have one of 3 values:
k=0 - flat universe The universe as a whole is Euclid and has zero curvature at every point.
k=1 - positive curvature At every point the universe has a positive curvature, that is, parallel geodesics converge at a distance. Unlike the two other types that are infinite (open) this type of geometry forms a closed universe. It has finite volume and the geodesics of it form giant circles. It is analogous to a 2D surface of a sphere.
k=-1 - negative curvature The curvature of the universe is negative. Parallel geodesics diverge at a distance. There is no 2D analogy for a space that has the same negative curvature at every point. A hyperboloid has negative curvature at every point but it is not homogenous.
The type of the universe geometry is determined by the ratio between the rate of expansion and the density. For a given rate of expansion there is a critical density for which the universe is flat. Lower density will result in negative curvature and higher density will cause positive curvature and a closed universe. The type of the geometry also determines the future of the universe. An open universe will continue to expand forever. A closed universe will stop expanding at a certain time and start contracting again. The observation done by now did not give a positive answer to the question what kind of geometry the universe has. It is known to be close to flat, but it might have a slight positive or negative curvature. When Einstein first used his GR theory for a model of the universe he assumed that the universe is static. To satisfy the GR equation with static universe Einstein had to add a new term to the equation called the cosmological constant. Without this term the universe would start contracting due to its own gravity. Later when Hubble discovered that the universe was expanding, what lead to the theory of the Big Bang, the cosmological constant wasn't needed anymore. It was well accepted that the matter in the universe was hurled in all direction by the Big Bang and since than it is expanding and the expansion keeps decelerating. Just before the end of the millennium observations have shown that the universe expansion is actually accelerating and not decelerating. The cosmological constant has been taken out of its grave to enable a solution for an accelerating universe. It is also referred to as the vacuum energy or dark energy.
|